Brownian Motion

Brownian motion describes the stochastic diffusion of particles as they travel through n-dimensional spaces filled with other particles and physical barriers. Here the term particle is a generic term that can be generalized to describe the motion of molecule (e.g. H₂O) or proteins (e.g. NMDA receptors); note however that stochastic diffusion can also apply to things like the price index of a stock (see random walk) or the propagation heat energy across a surface. Brownian motion is among the simplest continuous-time stochastic processes, and a limit of various probabilistic processes (see random walk). As such, Brownian motion is highly generalizable to many applications, and is directly related to the universality of the normal distribution. In some sense, stochastic diffusion is a pure actuation of the basic statistical properties of probability distributions - it is distribution sampling translated into movements.

Properties of Brownian Motion

Physical experiments characterize the following properties of Brownian motion...

• continuous increments
• increments of a particle over disjoint time intervals are independent events
• each increment is assumed to result from collisions with many molecules
• each increment is assumed to have a normal probability distribution
• the mean increment is zero as there is no preferred direction
• the position of a particle spreads out with time
• the variance of the increment is proportional to the length of time that Brownian motion has been observed

The probability density of a normally distributed random variable with mean μ and standard deviation σ is given by:

$f(x,\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}({\frac {x-\mu }{\sigma }})^{2}}$

Mathematically, the random process called Brownian motion is denoted here as B(t) and defined for times t ≥ 0; the probability density of Brownian particles at the end of time period [0, t] is obtained by substituting μ = 0 and σ = √t, giving:

${\frac {1}{\sqrt {t2\pi }}}e^{-{\frac {1}{2}}({\frac {x}{\sqrt {t}}})^{2}}$

where x denotes the value of random variable B(t). The probability distribution of the increment B(t + u) − B(t) is:

$P[B(t+u)-B(t)\leq a]=\int _{x=-\infty }^{a}{\frac {1}{\sqrt {u2\pi }}}e^{-{\frac {1}{2}}({\frac {x}{\sqrt {u}}})^{2}}dx$

Common Diffusion Terms & Parameters

I've found it most helpful to learn about the terms and parameters used to characterize stochastic diffusion as they apply to diffusion phenomena along a flat 2D surface. These parameters include:

D  : diffusion rate coefficient

$D={L^{2} \over 2d\cdot t}$

L : step length

d : dimensions

t : time

D (in units: µm²/s) is the mean diffusion rate per unit time (velocity), often in µm²/s for biological motion on a molecular level (n.b. µm²/s are the units for particle diffusion on a surface/membrane; the surface can actually be curved or ruffled such that the surface fills a 3D space, however the diffusion equations for those instances are slightly more complex. Units for 3D space are naturally: µm³/s). This refers to how fast, on average, the particle moves along its surface trajectories. This value is often of ultimate interest, that is, the goal of single-particle tracking studies is often to define the average diffusion rate of a molecule and report it as a Diffusion Coefficient; once D is known, this Diffusion Coefficient can then be easily implemented in computer simulations of Brownian motion. However under most circumstances, the diffusion rate cannot be observed directly in empirical experiments - this would require the ability to visualize all the microscopic particles and collisions that dictate the particle's movement on a nanosecond timescale. In the animation on the right, the diffusion rate can actually be quantified directly; but what is often seen when observing particle diffusion through a microscope would more closely resemble this:

Instead, D is often calculated from the mean squared diffusion (MSD) path of the particle, defined below.

MSD  : mean squared displacement

$MSD={2d\cdot D}$

d : dimensions

D : diffusion coefficient

MSD (in units: µm²) is the mean square displacement of a particle over some time period. If D (the diffusion coefficient) is unknown, MSD can be computed using the following equation:

Error creating thumbnail: File missing

...where the quantity 'x ' refers to the displacement of a particle over 'n ' total steps, with 'k ' indicating the current step.

Standard deviation (k) of the normal distribution of step lengths

$k={\sqrt {d\cdot D}}$

d : dimensions

D : diffusion coefficient

k (in units: µm) is the standard deviation (σ) of the normal distribution of step lengths that, when randomly sampled, will give rise to a diffusion rate D. This value is useful for simulating Brownian motion for a particular diffusion rate.

Mean Step Length (L)

$L={\sqrt {2d\cdot D}}$

d : dimensions

D : diffusion coefficient

L or Λ (in units: µm) is the average step length per interval of observation. In diffusion simulations, this is the step size per iteration (equivalent form: L = (2d * D).5).

Mean 1D step length component (λ)

$\lambda ={L \over {\sqrt {2}}}$

λ (in units: µm) is the average 1-dimensional step length for each component (X,Y,Z) dimension of L. For example, simulating 2D particle diffusion will require the generation of individual step lengths for both the X and Y dimension. The total step distance from the origin will be the length of the hypotenuse created by the individual X and Y component step lengths. In fact, the equation: λ = L / √2 is derived from the Pythagorean theorem for right triangles, such that 2λ² = λ² where 2λ² represents a² + b² and λ² represents c².

Step length scalar coefficient (ε)

$\epsilon ={\sqrt {\delta \over {D}}}$

δ : new desired diffusion rate

ε (in units: au) is a coefficient value that, when multiplied by each λ component step length, will scale those lengths to achieve a new diffusion rate δ.

Brownian Motion MATLAB Code

function [tracks] = BrownianMotion()


% STARTING PARAMETERS
%-----------------------------------------------------------
D = .3;                     % Diffusion Rate
Ds = .1;                    % Diffusion Scalar (Ds = Dn)
Dn = D/(D/Ds);              % new D after scaling L
d = 2;                      % dimensions
dT = 1;                     % time step
k = sqrt(d*D);	            % stdev of D's step size distribution
MSD = 2*d*D;                % mean squared displacement
L = sqrt(2*d*D);            % average diagonal (2D) step size
Lx = L/sqrt(2);             % average linear (1D) step size
Ls = 1/sqrt(D/Ds);          % scales Lx values for Dn


MSDtest = [1 0 0];			% test: D, Dn, or L
Scale = 1/10;				% scale of model
Ndots = 100;
Nsteps = Ndots;


xyl = ones(2,Ndots);
xyds = ones(2,Ndots);
lims = ((D+1)^2)*10;



% LIVE PARTICLE DIFFUSION
%-----------------------------------------------------------
for t = 1:Nsteps

    xyds = STEPxyds(Ndots, k);
	[xyl] = AMPARSTEP(Ndots, xyds, xyl);
	MAINPLOT(xyl, lims);

end




% MSD RANDOM STEPS ANALYSIS
%-----------------------------------------------------------
tracks = cell(Ndots, 1);

stepN = 1;
for t = 1:Nsteps 

	xyds = STEPxyds(Ndots, k);
	[xyl] = AMPARSTEP(Ndots, xyds, xyl);
    [tracks] = MSDfun(stepN, Nsteps, tracks, xyds);

stepN = stepN+1;
end
MSDfunction(tracks,Ndots,Nsteps,D,Dn,L,dT,k,Scale,MSDtest);



% MSD UNIFORM STEPS ANALYSIS
%-----------------------------------------------------------
stepN = 1;
for t = 1:Nsteps 

xyds = stepsize(Ndots, Lx);
		
	[xyl xyds] = MSDAMPARSTEP(Ndots, xyds, xyl, Ls);
    [tracks] = MSDfun(stepN, Nsteps, tracks, xyds);

stepN = stepN+1;
end
MSDfunction(tracks,Ndots,Nsteps,D,Dn,L,dT,k,Scale,MSDtest);

end



%%


% STEP SIZE GENERATOR
%-----------------------------------------------------------
function xyds = STEPxyds(Ndots, k)

    xyds = (k * randn(2,Ndots));

end



% MOVE PARTICLES MAIN FUNCTION
%-----------------------------------------------------------
function [xyl] = AMPARSTEP(Ndots, xyds, xyl)
	
	for j = 1:Ndots
        xyl(:,j) = xyl(:,j)+xyds(:,j);
	end
	
end



% LIVE DIFFUSION PLOT
%-----------------------------------------------------------
function [] = MAINPLOT(xyl, lims)

xlim = [-lims lims];
ylim = [-lims lims];
zlim = [-5 5];

figure(1)
subplot(2,1,1), 
AMPARPlot = gscatter(xyl(1,:),xyl(2,:));
axis([xlim, ylim]);
set(AMPARPlot,'marker','.','markersize',[6],'color',[1 0 0])

figure(1);
subplot(2,1,2), 
gscatter(xyl(1,:),xyl(2,:)); view(20, 30);
axis normal;
grid off
axis([xlim, ylim, zlim]);
set(gca, 'Box', 'on');

end



% MANUAL STEP SIZE FUNCTION
%-----------------------------------------------------------
function xyds = stepsize(Ndots, Lx)

   Lx(1:2,1:Ndots) = Lx;
   xyd = randi([0 1],Ndots,2)';
   xyd(xyd == 0) = -1;
   xyds = (Lx.*xyd);
   
end



% MSD SCALED STEPS FUNCTION
%-----------------------------------------------------------
function [xyl xyds] = MSDAMPARSTEP(Ndots, xyds, xyl, Ls)
	
	for j = 1:Ndots
        xyds(:,j) = xyds(:,j)*Ls;
        xyl(:,j) = xyl(:,j)+xyds(:,j);
	end	
	
end



% MSD TRACKS GENERATOR
%-----------------------------------------------------------
function [tracks] = MSDfun(stepN, Nsteps, tracks, xyds)

    time = (0:Nsteps-1)';
    xymsd = xyds';
    xymsd = cumsum(xymsd,1);
    tracks{stepN} = [time xymsd];

end



% MSD TRACKS ANALYSIS
%-----------------------------------------------------------
function [] = MSDfunction(tracks,Ndots,Nsteps,D,Dn,L,dT,k,Scale,MSDtest)

SPACE_UNITS = 'µm';
TIME_UNITS = 's';
N_PARTICLES = Ndots;
N_TIME_STEPS = Nsteps;
N_DIM = 2;

oD = D;				% raw		µm^2/s
D  = D*Scale;       % to-scale	µm^2/s

oDn = Dn;			% raw		µm^2/s
Dn = Dn*Scale;		% to-scale	µm^2/s

oL = L;				% raw		µm
L = L*Scale;		% to-scale	µm

dTbase = dT;		% raw time-step 
dT = dT*Scale;		% to-scale time-step
k = k;				% stdv of step distribution

ma = msdanalyzer(2, SPACE_UNITS, TIME_UNITS);
ma = ma.addAll(tracks);
disp(ma)

figure
ma.plotTracks;
ma.labelPlotTracks;

ma = ma.computeMSD;
ma.msd;

t = (0 : N_TIME_STEPS)' * dT;
[T1, T2] = meshgrid(t, t);
all_delays = unique( abs(T1 - T2) );

figure
ma.plotMSD;


cla
ma.plotMeanMSD(gca, true)

mmsd = ma.getMeanMSD;
t = mmsd(:,1);
x = mmsd(:,2);
dx = mmsd(:,3) ./ sqrt(mmsd(:,4));
errorbar(t, x, dx, 'k')

[fo, gof] = ma.fitMeanMSD;
plot(fo)
ma.labelPlotMSD;
legend off


ma = ma.fitMSD;

good_enough_fit = ma.lfit.r2fit > 0.8;
Dmean = mean( ma.lfit.a(good_enough_fit) ) / 2 / ma.n_dim;
Dstd  =  std( ma.lfit.a(good_enough_fit) ) / 2 / ma.n_dim;

Dheader1 = ['Raw Unscaled Values'];
Dhead1 = ['    D        Dn        L'];
Ddat1 = [oD oDn oL];
disp(' ')
disp(Dheader1)
disp(Dhead1)
disp(Ddat1)


yourtesthead = ['YOU ARE TESTING DIFFUSION FOR:'];
if MSDtest(1)
	yourtest = ['   D:   original diffusion rate'];
elseif MSDtest(2)
	yourtest = ['   Dn:  new diffusion rate'];
elseif MSDtest(3)
	yourtest = ['   L:  step length'];
else
	yourtest = ['   generic diffusion rate'];
end
disp(yourtesthead)
disp(yourtest)

disp(' ')
fprintf('Estimation of raw D coefficient from MSD:\n')
fprintf('D = %.3g ± %.3g (mean ± std, N = %d)\n', ...
    Dmean, Dstd, sum(good_enough_fit));




% Retrieve instantaneous velocities, per track
 trackV = ma.getVelocities;

 % Pool track data together
 TV = vertcat( trackV{:} );

 % Velocities are returned in a N x (nDim+1) array: [ T Vx Vy ...]. So the
 % velocity vector in 2D is:
 V = TV(:, 2:3);

 % Compute diffusion coefficient
varV = var(V);
mVarV = mean(varV); % Take the mean of the two estimates
Dest = mVarV / 2 * dT;



Dheader2 = ['Scaling to model...'];
Dhead2 = ['    D        Dn        L'];
Ddat2 = [D Dn L];

disp(' ')
disp(Dheader2)
disp(Dhead2)
disp(Ddat2)
fprintf('Estimation from velocities histogram:\n')
fprintf('Tested D = %.3g %s, compare to scaled Des value of %.3g %s\n', ...
    Dest, [SPACE_UNITS '²/' TIME_UNITS], D, [SPACE_UNITS '²/' TIME_UNITS]);

% printf('D.psd target value was %.3g %s\n', ...
%     Dest, msdDpsd, [SPACE_UNITS '²/' TIME_UNITS]);

end

Stochastic Diffusion

This exercise shows how to simulate the motion of single and multiple particles in one and two dimensions using Matlab. You will discover some useful ways to visualize and analyze particle motion data, as well as learn the Matlab code to accomplish these tasks. Once you understand the simulations, you can tweak the code to simulate the actual experimental conditions you choose for your study of Brownian motion of synthetic beads. These simulations will generate the predictions you can test in your experiment.

In each section, Matlab code shown in the box to the left is used to generate the plot or analysis shown on the right. To use the code, copy it from the box on the left, launch the Matlab application, and paste the code into the Matlab Command Window. If you are new to Matlab, check out the Intro to Matlab page to help you get started.

Simulating Single Particle Trajectories

The following sections cover simulating the stochastic motion of individual particles in n-dimensions.

For a tutorial on using the Matlab MSD extension see: Mean Squared Diffusion (MSD) Tutorial

Open Source 'plasticity' Project

Before jumping into the fundamentals of stochastic diffusion programming, it may be encouraging to know that these basic principles can be combined to model stochastic processes with real-world applications. One current project I'd like to plug is called "plasticity", which is an open source collaboration I started last year aimed at modeling the membrane diffusion of receptors along dendritic surfaces of neurons. The overall goal of "plasticity" is to develop spatially and temporally accurate models of molecular dynamics in neurons, and simulate complex activities using simple MCMC and statistical method Here's a simulation produced using code from the plasticity repo on github.

One Dimensional Brownian Motion

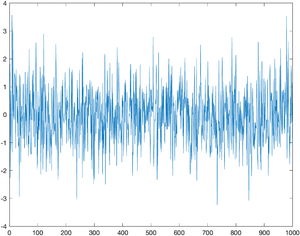
Brownian motion in one dimension is composed of a sequence of normally distributed random displacements. The randn function returns a matrix of a normally distributed random numbers with standard deviation 1. The two arguments specify the size of the matrix, which will be 1xN in the example below.

The first step in simulating this process is to generate a vector of random displacements. The commands to do this are shown below. N is the number of samples to generate.

%-------------############################------------------%
%                 One Dimensional Brownian Motion
%-------------############################------------------%

N = 1000;
displacement = randn(1,N);
plot(displacement);

%-------------############################------------------%

Distribution of Displacements

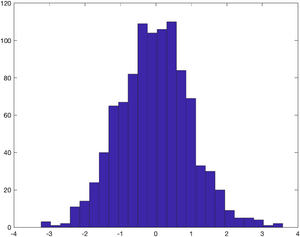
Have a look at the distribution of the randomly generated displacements. The hist command plots a histogram of the values. The second argument - 25 - specifies that Matlab should divide the values into 25 bins.

hist(displacement, 25);

Convert displacements to position

Now we have some appropriate random displacements. Their sum represents a particle trajectory in 1 dimension. The Matlab function cumsum returns the cumulative sum of a vector. The following commands take the cumulative sum of displacement and save the result in a vector called x.

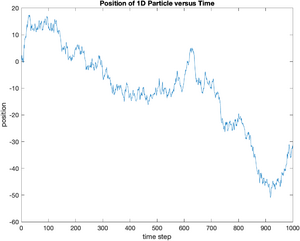
x = cumsum(displacement);
plot(x);
ylabel('position');
xlabel('time step');
title('Position of 1D Particle versus Time');

Two dimensional particle simulation

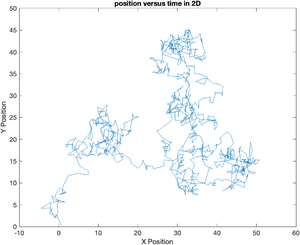
Extending this to two dimensions is simple. Since all directions are (assumed to be) equivalent, all we need to do is generate two vectors of random displacements. The vector of displacements saved in a Matlab structure called particle. x and y position vectors are stored in members of the structure. This data could also have been saved as a 2xN matrix. Using a structure has the important advantage that a meaningful name can be assigned to each member. This good practice makes your code much more readable.

%-------------###############################----------------%
%             Two Dimensional Brownian Motion
%-------------###############################----------------%

particle = struct();
particle.x = cumsum( randn(N, 1) );
particle.y = cumsum( randn(N, 1) );

plot(particle.x, particle.y);
  ylabel('Y Position');
  xlabel('X Position');
  title('position versus time in 2D');

%-------------############################------------------%

Compute the Displacement Squared

The displacement squared is equal to the x coordinate squared plus the y coordinate squared. Since the simulated particle always start at (0,0), it is unnecessary to subtract off the initial position (as will be necessary with the data you gather in the lab).

The dot caret (.^) operator raises each element of a matrix to a power.

dsquared = particle.x .^ 2 + particle.y .^ 2;
plot(dsquared);

Theoretical Value of D

The theoretical value of the diffusion coefficient, D, is given by D = kB * T / (3πrη) where T = temperature (Kelvin), k_B = Boltzmann's constant, eta = viscosity, and r = diffusion_radius.

Note that the units of D are length squared divided by time. See the lab writeup for more information. Let's compute D for a 1 micron particle in water at 293 degrees Kelvin.

r    = 1.0e-6;              % radius in meters
eta  = 1.0e-3;              % viscosity of water in SI units (Pascal-seconds) at 293 K
kB   = 1.38e-23;            % Boltzmann constant
T    = 293;                 % Temperature in degrees Kelvin

D    = kB * T / (3 * pi * r * eta)

ans =
      4.29e-13

Qian et al. derived a way to estimate the diffusion coefficient from the distribution of instantaneous velocities. If v is the instantaneous velocity vector, then

(v) = 2D / dT

A more realistic particle -- Getting the Units Right

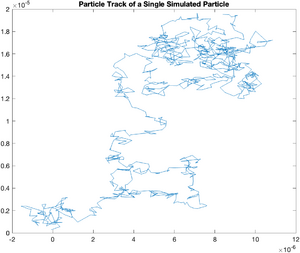
So far, we have been looking at simulated particles with a mean squared displacement of 1 unit per time interval. To accurately model a real particle, it is necessary to adjust the distribution of random displacements to match the experimental conditions.

According to theory, the mean squared displacement of the particle is proportional to the time interval, where r(t) = position, d = number of dimensions, D = diffusion coefficient, and tau = time interval.

To generate the correct distribution, the output from randn (which has a standard normal distribution) must be scaled by the factor k.

%-------------###############################----------------%
%             Two Dimensional Realistic Brownian Motion
%-------------###############################----------------%

dimensions = 2;         % two dimensional simulation
tau = .1;               % time interval in seconds
time = tau * 1:N;       % create a time vector for plotting

k = sqrt(D * dimensions * tau);
dx = k * randn(N,1);
dy = k * randn(N,1);

x = cumsum(dx);
y = cumsum(dy);

dSquaredDisplacement = (dx .^ 2) + (dy .^ 2);
 squaredDisplacement = ( x .^ 2) + ( y .^ 2);

plot(x,y);
title('Particle Track of a Single Simulated Particle');

%-------------############################------------------%

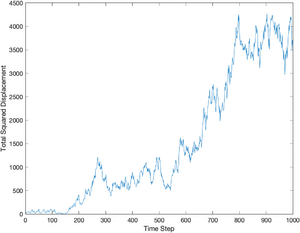
Displacement Squared Plot

Theory predicts that the displacement should increase in proportion to the square root of time. The theoretical value of displacement squared is plotted with a thick black line. Since displacement is expected to increase with the square root of time, displacement squared is a straight line in the plot. With only a single particle and a small number of samples, deviation from the line can be quite large.

clf;
hold on;
plot(time, (0:1:(N-1)) * 2*k^2 , 'k', 'LineWidth', 3);      % plot theoretical line

plot(time, squaredDisplacement);
hold off;
xlabel('Time');
ylabel('Displacement Squared');
title('Displacement Squared versus Time for 1 Particle in 2 Dimensions');

Estimating D from the Simulated Data

The best estimate of the value of D from the simulated data is:

simulatedD = mean( dSquaredDisplacement ) / ( 2 * dimensions * tau )

ans = 
     4.2192e-013

Uncertainty in the Estimate

The likely error of this measurement decreases as the square root of the number of samples. This will be discussed in more detail later.

standardError = std( dSquaredDisplacement ) / ( 2 * dimensions * tau * sqrt(N) )
actualError = D - simulatedD

standardError = 
               1.3162e-014

actualError   = 
               7.1019e-015

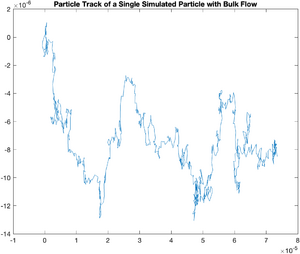
Systematic Error -- Bulk Flow in the Solvent

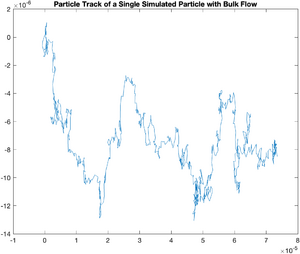
Sometimes, evaporation or uneven heating of the solvent will cause a flow to occur on the slide you are observing. We can model this easily. The following code models a flow with a magnitude 0.5 k in the x direction and 0.1 k in the y direction.

dx = dx + 0.2 * k;
dy = dy + 0.05 * k;

x = cumsum(dx);
y = cumsum(dy);

dSquaredDisplacement = (dx .^ 2) + (dy .^ 2);
 squaredDisplacement = ( x .^ 2) + ( y .^ 2);

simulatedD    = mean( dSquaredDisplacement ) / ( 2 * dimensions * tau )
standardError = std(  dSquaredDisplacement ) / ( 2 * dimensions * tau * sqrt(N) )
actualError = D - simulatedD

plot(x,y);
title('Particle Track of a Single Simulated Particle with Bulk Flow');

simulatedD    =  
               4.2926e-013
standardError =  
               1.3694e-014
actualError   = 
              -2.3859e-016

Displacement Squared in the Presence of Bulk Flow

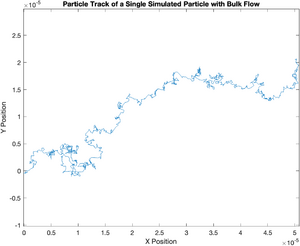
Notice how the plot of displacement squared diverges from the theoretical value. It has a distinct quadratic component. The magnitude of this error increases dramatically with time. This suggests that the error caused by bulk flow can be minimized by using the shortest possible sampling period. But there's a catch. As you increase the sampling rate, the amount of noise from the motion tracking algorithm goes up. A tenth of a second works pretty well for the particles you will observe in the lab. If you have time, take a few movies at a different rates to see the effect.

clf;
hold on;
plot(time, (0:1:(N-1)) * 2*k^2 , 'k', 'LineWidth', 3);      % plot theoretical line
plot(time, squaredDisplacement);
hold off;

xlabel('Time');
ylabel('Displacement Squared');
title('Displacement Squared versus Time with Bulk Flow');

Simulating Multiple Particles

When you take your data in the lab, you will make movies of many particles. You will use a Matlab program to extract particle tracks from these movies. Because particles drift out of view and go in and out of focus, most movies will be about 5 seconds long at a sample rate of 10 Hz or so. Let's simulate this.

Using a For Loop to Generate Multiple Data Sets

A for loop is the key to generating multiple particle simulations. The results of the simulations are stored in a cellular array of structures called particle. For example, particle{3} refers to a structure containing the results of simulation number 3. particle{3}.D is the estimated value of D for simulation number 3. It is not necessary to understand this code in depth. But do yourself a favor and have a look.

particleCount = 10;
N = 50;
tau = .1;
time = 0:tau:(N-1) * tau;
particle = { };             % create an empty cell array to hold the results

for i = 1:particleCount
    particle{i} = struct();
    particle{i}.dx = k * randn(1,N);
    particle{i}.x = cumsum(particle{i}.dx);
    particle{i}.dy = k * randn(1,N);
    particle{i}.y = cumsum(particle{i}.dy);
    particle{i}.drsquared = particle{i}.dx .^2 + particle{i}.dy .^ 2;
    particle{i}.rsquared = particle{i}.x .^ 2 + particle{i}.y .^ 2;
    particle{i}.D = mean( particle{i}.drsquared ) / ( 2 * dimensions * tau );
    particle{i}.standardError = std( particle{i}.drsquared ) / ( 2 * dimensions * tau * sqrt(N) );
end

SimulateParticle Function

That's a lot of typing. Fortunately, all of the commands to generate multiple particle tracks have been combined into in a single function called SimulateParticles. If you are interested in how the function is implemented, type edit SimulateParticles.m to have a look at the m-file for this function.

help SimulateParticles

particle = SimulateParticles(N, particleCount, tau, k);
 
usage: out = 
SimulateParticles( N, particleCount, tau, k )

N is the number of samples
particleCount is the number of particles
tau is the sample period
k is the standard deviation of dx and dy
 
returns a cellular array of length particleCount

Look at the Results

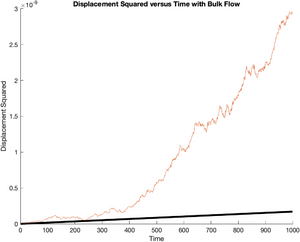
The following code plots all of the generated particle tracks on a single set of axes, each in a random color.

clf;
hold on;
for i = 1:particleCount
    plot(particle{i}.x, particle{i}.y, 'color', rand(1,3));
end

xlabel('X position (m)');
ylabel('Y position (m)');
title('Combined Particle Tracks');
hold off;

Displacement Squared

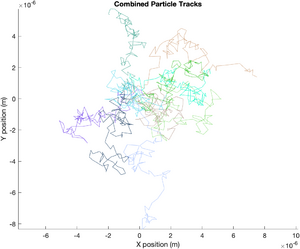
The following plot shows displacement squared versus time for all of the particles. The ensemble average of all the displacements is shown with a thick black line. The theoretical value of displacement squared is plotted with a thick blue line. Since displacement is expected to increase with the square root of time, displacement squared is a straight line in the plot.

% compute the ensemble average
rsquaredSum = zeros(1,N);

for i = 1:particleCount
    rsquaredSum = rsquaredSum + particle{i}.rsquared;
end

ensembleAverage = rsquaredSum / particleCount;

% create the plot
clf;
hold on;
plot(time, (0:1:(N-1)) * 2*k^2 , 'b', 'LineWidth', 3);      % plot theoretical line

plot(time, ensembleAverage , 'k', 'LineWidth', 3);          % plot ensemble average
legend('Theoretical','Average','location','NorthWest');

for i = 1:particleCount
    plot(time, particle{i}.rsquared, 'color', rand(1,3));   % plot each particle track
end

xlabel('Time (seconds)');
ylabel('Displacement Squared (m^2)');
title('Displacement Squared vs Time');
hold off;

Estimated Value of D

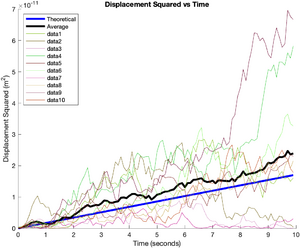
This plot shows the computed value of D for each simulation with error bars. A thick blue line indicates the best overall estimate of D (the average of the D value from each simulation) along with error bars in green * WHICH HAPPEN TO BE WRONG -- NEED TO FIX *.

clear D e dx;

% extract the D value from each simulation and place them all into a single
% matrix called 'D'
for i = 1:particleCount
    D(i) = particle{i}.D;
    dx(i,:) = particle{i}.dx;
    e(i) = particle{i}.standardError;
end

% compute the estimate of D and the uncertainty
averageD = mean(D)
uncertainty = std(D)/sqrt(particleCount)

% plot everything
clf;
hold on;

plot(averageD * ones(1,particleCount), 'b', 'linewidth', 3);                    % plot estimated D
plot((averageD + uncertainty) * ones(1,particleCount), 'g-', 'linewidth', 1);   % plot upper error bar
plot((averageD - uncertainty) * ones(1,particleCount), 'g-', 'linewidth', 1);   % plot lower error bar
errorbar(D,e,'ro');                                                             % plot D values with error bars

xlabel('Simulation Number');
ylabel('Estimated Diffusion Coefficient');
title('Estimated Diffusion Coefficient with Error Bars')
legend('Average Value of D', 'location', 'NorthWest');

hold off;

averageD    = 
             4.2886e-013

uncertainty = 
             2.3294e-014

Fancy Statistics and Plots

This section looks at the statistical properties of the simulated data in more detail. In particular, it discusses:

• Uncertainty in the estimate of the mean value of a random variable from a population of samples
• The effect of squaring a normally distributed random variable
• The assumption of statistical independence of samples

A More Perfect Distribution

Error creating thumbnail: File missing

Error creating thumbnail: File missing

Did you notice that the distribution of random displacement values in the second section looked a little lopsided? Even with 1000 samples, there can be some noticeable deviations from the ideal distribution. A million samples looks quite a bit closer to the ideal.

hist(randn(1,1e3),25)
xlabel('Value');
ylabel('Frequency');
title('Histogram of Values for 1000 Samples of randn');

hist(randn(1,1e6),100)
xlabel('Value');
ylabel('Frequency');
title('Histogram of Values for 1000000 Samples of randn');

Sampling Uncertainty

Error creating thumbnail: File missing

This lab requires you to make an estimate of the average value of a random variable (actually, the square of a random variable) from a population of samples of that variable. The uncertainty in your estimate decreases with the square root of the number of samples, N. (That is, the standard error = 1/sqrt(N).)

This concept is illustrated in the following plot. To create the plot, fifty populations of N random samples are created for each value of N from 1 to 100. The mean value of each sample population is plotted with an 'x' versus N. The uncertainty appears to decrease as 1/sqrt(N) as expected. About two thirds of the values fall between the error bars (plotted in dark black).

Matlab note: check out the nested for loops used to create the plot.

clf; hold on;
for i= 1:100
    for j = 1:50
        y = randn(1,i);
        m = mean(y);
        plot(i,m,'x');
    end
end

plot(1:100, 1./sqrt(1:100), 'k', 'LineWidth', 2);   % plot upper error bar in dark black
plot(1:100, -1./sqrt(1:100), 'k', 'LineWidth', 2);  % plot lower error bar in dark black
hold off;
xlabel('Population Size (N)');
ylabel('Population Mean');
title('Population Mean of Normally Distributed Random Variable versus Population Size');

What Happens when you Square a Random Variable?

Error creating thumbnail: File missing

We did not estimate D in the simulations from the x and y displacements directly. Instead, we computed the mean squared value of dx and dy. What is the distribution of the resulting value? Adding the squares of two normally distributed random variables results in a chi-squared distribution (with two degrees of freedom) whose mean value equal to the sum of the variances of each variable. Here is what the chi-squared distribution looks like:

dx = randn(1,1e6);
dy = randn(1,1e6);
drSquared = dx .^ 2 + dy .^ 2;

mean(drSquared)
var(dx) + var(dy)

clf;
hist(drSquared,100);
title('Chi Squared Distribution (2 DOF), 1000000 Samples');

ans = 
    1.9982

ans = 
    1.9982

100 Years of BIO Lab Data in 1 Second

Error creating thumbnail: File missing

So does the uncertainty of the squared and summed behave as expected? The following plot is a simulation of 5000 data sets - 50 at each value of N just as above. (This is what a plot of all the data from students doing the BIO lab for the next hundred years might look like. Some lazy groups decided to use very low values of N.)

clf;
hold on;

for i= 1:100
    for j = 1:50
        dx = randn(1,i);
        dy = randn(1,i);
        m = mean( dx .^ 2 + dy .^ 2 );
        plot(i,m,'x');
    end
end

plot(1:100, 2 + 2./sqrt(1:100), 'k', 'LineWidth', 2);  % plot upper error bar in dark black
plot(1:100, 2 - 2./sqrt(1:100), 'k', 'LineWidth', 2);  % plot lower error bar in dark black

hold off;
xlabel('Population Size (N)');
ylabel('Population Mean');
title('Population Mean of Chi Squared (2 DOF) Distributed Random Variable versus Population Size');

Planning Your Time in the Lab

Sampling error sets a lower bound on the uncertainty in your estimate of the diffusion coefficient from experimental data. To plan your time in the lab, it will be important to understand how much data you should take for each experimental condition. Because the particles go out of focus and drift away from of the observation area, it can be difficult to make movies longer than about 5 seconds. At a frame rate of 10 frames per second, how many movies would you have to make to achieve a final uncertainty of 10%? 1%? .1%? What level of uncertainty will you try for in the lab?

Auto Correlation - A Closer Look at the Data

Error creating thumbnail: File missing

The simulations so far have assumed that we are in the overdamped limit, or the inertia-less regime. This assumption makes generating simulated trajectories very easy - all you have to do is add up a bunch of properly distributed random numbers. Of course, just because something is convenient doesn't mean it's true.

There are many statistical tests for independence and normality. (My personal favorite is the Kolmogorov-Smirnov test – but never before 5:00 PM.) Auto and cross correlation are a good place to start testing for independence. Autocorrelation looks for a relationship between a variable and its past or future values. Cross correlation looks for a relationship between two variables. Matlab has a built in function to compute auto and cross correlations called xcorr.

By construction, the simulated displacements are independent. The change in position at one time should exhibit no relationship at all to the change at any other time. This can be verified with xcorr. If x is a vector, xcorr(x) returns the correlation of x with itself for all possible offsets. The length of the resulting autocorrelation sequence is 2N+1. The middle value always stands out because x correlates perfectly with itself when there is no offset. Specifying the option 'coeff' causes the xcorr function to normalize this value to exactly 1 --perfect correlation.

Also notice that the autocorrelation sequence is symmetric about the origin.

clf;
c = xcorr(particle{1}.dx, 'coeff');
xaxis = (1-length(c))/2:1:(length(c)-1)/2;

plot(xaxis, c);
xlabel('Lag');
ylabel('Correlation');
title('Particle 1 x-axis Displacement Autocorrelation');

Cross Correlation

Error creating thumbnail: File missing

With two vector arguments, xcorr(x,y) returns a cross correlation matrix. The cross correlation can be used to test the relationship (or lack thereof) between one particle's trajectory and another's. If two particles move independently, the cross correlations should be very small. The code below computes the cross correlation between the x displacements of particle simulations number 1 and 2.

clf;
c = xcorr(particle{1}.dx, particle{2}.dx, 'coeff');
xaxis = (1-length(c))/2:1:(length(c)-1)/2;
plot(xaxis, c);
xlabel('Lag');
ylabel('Correlation');
Title('Particle 1, 2 x-axis Displacement Cross Correlation');

MATLAB Tricks

Error creating thumbnail: File missing

Matlab can generate (and plot) an amazing amount of data. For example, the xcorr function can compute the auto and cross correlations of a large set of data values. If A is an MxN matrix, xcorr(A) returns a size 2*M-1 x N^2 matrix whose columns contain the cross-correlation sequences for all combinations of the columns of A. The football shape of the data is a result of the way that the data is windowed when computing the correlation.

% create an array whose columns contain the dx values for each particle

for i = 1:particleCount
    allDx(:,i) = particle{i}.dx';
end

% compute all possible auto and cross correlations

c = xcorr(allDx, 'coeff');

% plot the results
clf;
hold on;
for i=1:size(c,1)
    plot(xaxis, c(:,i),'color',rand(1,3));
end
hold off;

xlabel('Lag');
ylabel('Correlation Coefficient');
title('All Possible Auto and Cross Correlations in the x Dimension');

A Correlated Trajectory

Error creating thumbnail: File missing

So what does the autocorrelation sequence look like for a trajectory that is not generated from independent samples? In the following example, the displacement at each time interval depends in part on the displacement in the last interval plus a random number. The autocorrelation is not nearly as sharp as the one generated by independent random samples.

x     = zeros(1,N);
c     = 0.80;           % degree of correlation; 0 to 1
step  = randn(1,N);
x(2) = randn();

for t=2:N
     x(t) = (c * x(t-1)) + ((1-c)*step(t));
end;

clf;
plot(xaxis, xcorr(x, 'coeff'));

xlabel('Lag');
ylabel('Correlation Coefficient');
title('Autocorrelation');

notes & articles

Here are several good resources for explaining and calculating MSD:

• wolfram alpha
• Democritus
• Matlab toolbox
• Mean Square Displacement Analysis of Single-Particle Trajectories with Localization Error: Brownian Motion in Isotropic Medium
• Active diffusion positions the nucleus in mouse oocytes

See Also

• Stochastic Diffusion