Brownian Motion

Brownian motion describes the stochastic diffusion of particles as they travel through n-dimensional spaces filled with other particles and physical barriers. Here the term particle is a generic term that can be generalized to describe the motion of molecule (e.g. H2O) or proteins (e.g. NMDA receptors); note however that stochastic diffusion can also apply to things like the price index of a stock (see random walk) or the propagation heat energy across a surface. Brownian motion is among the simplest continuous-time stochastic processes, and a limit of various probabilistic processes (see random walk). As such, Brownian motion is highly generalizable to many applications, and is directly related to the universality of the normal distribution. In some sense, stochastic diffusion is a pure actuation of the basic statistical properties of probability distributions - it is distribution sampling translated into movements.
Properties of Brownian Motion
Physical experiments characterize the following properties of Brownian motion...
- continuous increments
- increments of a particle over disjoint time intervals are independent events
- each increment is assumed to result from collisions with many molecules
- each increment is assumed to have a normal probability distribution
- the mean increment is zero as there is no preferred direction
- the position of a particle spreads out with time
- the variance of the increment is proportional to the length of time that Brownian motion has been observed
The probability density of a normally distributed random variable with mean μ and standard deviation σ is given by:
Mathematically, the random process called Brownian motion is denoted here as B(t) and defined for times t ≥ 0; the probability density of Brownian particles at the end of time period [0, t] is obtained by substituting μ = 0 and σ = √t, giving:
where x denotes the value of random variable B(t). The probability distribution of the increment B(t + u) − B(t) is:
Common Diffusion Terms & Parameters
I've found it most helpful to learn about the terms and parameters used to characterize stochastic diffusion as they apply to diffusion phenomena along a flat 2D surface. These parameters include:
D : diffusion rate coefficient
L: step lengthd: dimensionst: time
D (in units: µm²/s) is the mean diffusion rate per unit time (velocity), often in µm²/s for biological motion on a molecular level (n.b. µm²/s are the units for particle diffusion on a surface/membrane; the surface can actually be curved or ruffled such that the surface fills a 3D space, however the diffusion equations for those instances are slightly more complex. Units for 3D space are naturally: µm³/s). This refers to how fast, on average, the particle moves along its surface trajectories. This value is often of ultimate interest, that is, the goal of single-particle tracking studies is often to define the average diffusion rate of a molecule and report it as a Diffusion Coefficient; once D is known, this Diffusion Coefficient can then be easily implemented in computer simulations of Brownian motion. However under most circumstances, the diffusion rate cannot be observed directly in empirical experiments - this would require the ability to visualize all the microscopic particles and collisions that dictate the particle's movement on a nanosecond timescale. In the animation on the right, the diffusion rate can actually be quantified directly; but what is often seen when observing particle diffusion through a microscope would more closely resemble this:
Instead, D is often calculated from the mean squared diffusion (MSD) path of the particle, defined below.
Mean Squared Displacement (MSD)
d: dimensionsD: diffusion coefficient
MSD (in units: µm²) is the mean square displacement of a particle over some time period.
Standard deviation (k) of the normal distribution of step lengths
d: dimensionsD: diffusion coefficient
k (in units: µm) is the standard deviation (σ) of the normal distribution of step lengths that, when randomly sampled, will give rise to a diffusion rate D. This value is useful for simulating Brownian motion for a particular diffusion rate.
Mean Step Length (L)
d: dimensionsD: diffusion coefficient
L or Λ (in units: µm) is the average step length per interval of observation. In diffusion simulations, this is the step size per iteration (equivalent form: L = (2d * D).5).
Mean 1D step length component (λ)
λ (in units: µm) is the average 1-dimensional step length for each component (X,Y,Z) dimension of L. For example, simulating 2D particle diffusion will require the generation of individual step lengths for both the X and Y dimension. The total step distance from the origin will be the length of the hypotenuse created by the individual X and Y component step lengths. In fact, the equation: λ = L / √2 is derived from the Pythagorean theorem for right triangles, such that 2λ² = λ² where 2λ² represents a² + b² and λ² represents c².
Step length scalar coefficient (ε)
δ: new desired diffusion rate
ε (in units: au) is a coefficient value that, when multiplied by each λ component step length, will scale those lengths to achieve a new diffusion rate δ.
Brownian Motion MATLAB Code
Visit this page to view or download a full Brownian Motion simulation and analysis in MATLAB.
Simulating Particle Trajectories
This exercise shows how to simulate the motion of single and multiple particles in one and two dimensions using MATLAB. You will discover some useful ways to visualize and analyze particle motion data, as well as learn the Matlab code to accomplish these tasks. Once you understand the simulations, you can tweak the code to simulate the actual experimental conditions you choose for your study of Brownian motion of synthetic beads. These simulations will generate the predictions you can test in your experiment. In each section, MATLAB code shown in the box to the left is used to generate the plot or analysis shown on the right.
One Dimensional Brownian Motion
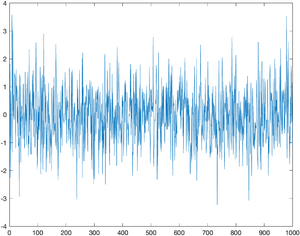
Brownian motion in one dimension is composed of a sequence of normally distributed random displacements. The randn function returns a matrix of a normally distributed random numbers with standard deviation 1. The two arguments specify the size of the matrix, which will be 1xN in the example below.
The first step in simulating this process is to generate a vector of random displacements. The commands to do this are shown below. N is the number of samples to generate.
% One Dimensional Brownian Motion
N = 1000;
displacement = randn(1,N);
plot(displacement);
Distribution of Displacements
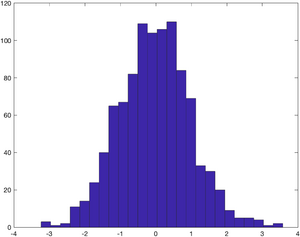
Have a look at the distribution of the randomly generated displacements. The hist command plots a histogram of the values. The second argument - 25 - specifies that Matlab should divide the values into 25 bins.
hist(displacement, 25);
Convert displacements to position
Now we have some appropriate random displacements. Their sum represents a particle trajectory in 1 dimension. The Matlab function cumsum returns the cumulative sum of a vector. The following commands take the cumulative sum of displacement and save the result in a vector called x.
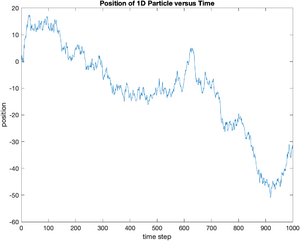
x = cumsum(displacement);
plot(x);
ylabel('position');
xlabel('time step');
title('Position of 1D Particle versus Time');
Two dimensional particle simulation
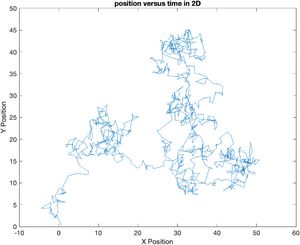
Extending this to two dimensions is simple. Since all directions are (assumed to be) equivalent, all we need to do is generate two vectors of random displacements. The vector of displacements saved in a Matlab struct called particle. x and y position vectors are stored in members of the structure. This data could also have been saved as a 2xN matrix. Using a structure has the important advantage that a meaningful name can be assigned to each member. This good practice makes your code much more readable.
% Two Dimensional Brownian Motion
particle = struct();
particle.x = cumsum( randn(N, 1) );
particle.y = cumsum( randn(N, 1) );
plot(particle.x, particle.y);
ylabel('Y Position');
xlabel('X Position');
title('position versus time in 2D');
Compute the Displacement Squared
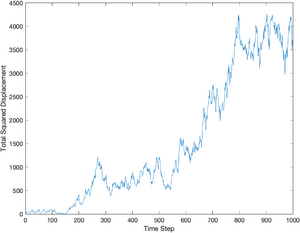
The displacement squared is equal to the x coordinate squared plus the y coordinate squared. Since the simulated particle always start at (0,0), it is unnecessary to subtract off the initial position (as will be necessary with the data you gather in the lab).
The dot caret (.^) operator raises each element of a matrix to a power.
% Displacement Squared
dsquared = particle.x .^ 2 + particle.y .^ 2;
plot(dsquared);
Theoretical Value of D
The theoretical value of the diffusion coefficient, D, is given by D = kB * T / (3πrη) where T = temperature (Kelvin), kB = Boltzmann's constant, eta = viscosity, and r = diffusion_radius. Note that the units of D are length squared divided by time. See the lab writeup for more information. Let's compute D for a 1 micron particle in water at 293 degrees Kelvin.
r = 1.0e-6; % radius in meters
eta = 1.0e-3; % viscosity of water in SI units (Pascal-seconds) at 293 K
kB = 1.38e-23; % Boltzmann constant
T = 293; % Temperature in degrees Kelvin
D = kB * T / (3 * pi * r * eta);
Qian et al. derived a way to estimate the diffusion coefficient from the distribution of instantaneous velocities. If v is the instantaneous velocity vector, then
v = 2D / dT
A more realistic particle -- Getting the Units Right
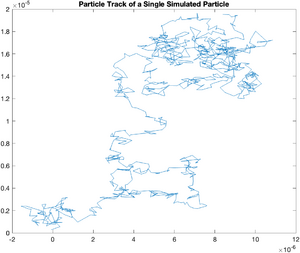
So far, we have been looking at simulated particles with a mean squared displacement of 1 unit per time interval. To accurately model a real particle, it is necessary to adjust the distribution of random displacements to match the experimental conditions.
According to theory, the mean squared displacement of the particle is proportional to the time interval, where r(t) = position, d = number of dimensions, D = diffusion coefficient, and tau = time interval.
To generate the correct distribution, the output from randn (which has a standard normal distribution) must be scaled by the factor k.
N = 1000;
r = 1.0e-6; % radius in meters
eta = 1.0e-3; % viscosity of water in SI units (Pascal-seconds) at 293 K
kB = 1.38e-23; % Boltzmann constant
T = 293; % Temperature in degrees Kelvin
D = kB * T / (3 * pi * r * eta);
dimensions = 2; % two dimensional simulation
tau = .1; % time interval in seconds
time = tau * 1:N; % create a time vector for plotting
k = sqrt(D * dimensions * tau);
dx = k * randn(N,1);
dy = k * randn(N,1);
x = cumsum(dx);
y = cumsum(dy);
dSquaredDisplacement = (dx .^ 2) + (dy .^ 2);
squaredDisplacement = ( x .^ 2) + ( y .^ 2);
plot(x,y);
title('Particle Track of a Single Simulated Particle');
Displacement Squared Plot
Theory predicts that the displacement should increase in proportion to the square root of time. The theoretical value of displacement squared is plotted with a thick black line. Since displacement is expected to increase with the square root of time, displacement squared is a straight line in the plot. With only a single particle and a small number of samples, deviation from the line can be quite large.
% continuing from above...
clf;
plot(time, (0:1:(N-1)) * 2*k^2 , 'k', 'LineWidth', 3); % plot theoretical line
hold on;
plot(time, squaredDisplacement);
hold off;
xlabel('Time');
ylabel('Displacement Squared');
title('Displacement Squared versus Time for 1 Particle in 2 Dimensions');
Estimating D from the Simulated Data
The best estimate of the value of D from the simulated data is:
simulatedD = mean( dSquaredDisplacement ) / ( 2 * dimensions * tau )
ans =
4.22 E-13
Uncertainty in the Estimate
The likely error of this measurement decreases as the square root of the number of samples. This will be discussed in more detail later.
standardError = std( dSquaredDisplacement ) / ( 2 * dimensions * tau * sqrt(N) )
actualError = D - simulatedD
standardError =
1.3162e-014
actualError =
7.1019e-015
Systematic Error -- Bulk Flow in the Solvent
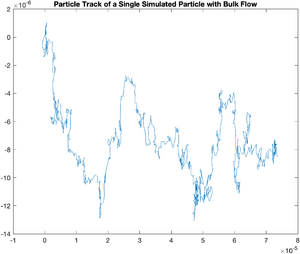
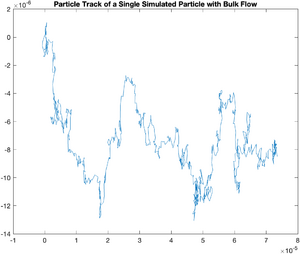
Sometimes, evaporation or uneven heating of the solvent will cause a flow to occur on the slide you are observing. We can model this easily. The following code models a flow with a magnitude 0.5 k in the x direction and 0.1 k in the y direction.
dx = dx + 0.2 * k;
dy = dy + 0.05 * k;
x = cumsum(dx);
y = cumsum(dy);
dSquaredDisplacement = (dx .^ 2) + (dy .^ 2);
squaredDisplacement = ( x .^ 2) + ( y .^ 2);
simulatedD = mean( dSquaredDisplacement ) / ( 2 * dimensions * tau )
standardError = std( dSquaredDisplacement ) / ( 2 * dimensions * tau * sqrt(N) )
actualError = D - simulatedD
plot(x,y);
title('Particle Track of a Single Simulated Particle with Bulk Flow');
simulatedD =
4.2926e-013
standardError =
1.3694e-014
actualError =
-2.3859e-016
Displacement Squared in the Presence of Bulk Flow
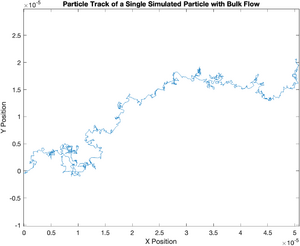
Notice how the plot of displacement squared diverges from the theoretical value. It has a distinct quadratic component. The magnitude of this error increases dramatically with time. This suggests that the error caused by bulk flow can be minimized by using the shortest possible sampling period. But there's a catch. As you increase the sampling rate, the amount of noise from the motion tracking algorithm goes up. A tenth of a second works pretty well for the particles you will observe in the lab. If you have time, take a few movies at a different rates to see the effect.
clf;
hold on;
plot(time, (0:1:(N-1)) * 2*k^2 , 'k', 'LineWidth', 3); % plot theoretical line
plot(time, squaredDisplacement);
hold off;
xlabel('Time');
ylabel('Displacement Squared');
title('Displacement Squared versus Time with Bulk Flow');
Simulating Multiple Particles
When you take your data in the lab, you will make movies of many particles. You will use a Matlab program to extract particle tracks from these movies. Because particles drift out of view and go in and out of focus, most movies will be about 5 seconds long at a sample rate of 10 Hz or so. Let's simulate this.
Using a For Loop to Generate Multiple Data Sets
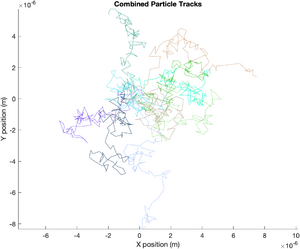
A for loop is the key to generating multiple particle simulations. The results of the simulations are stored in a cellular array of structures called particle. For example, particle{3} refers to a structure containing the results of simulation number 3. particle{3}.D is the estimated value of D for simulation number 3. It is not necessary to understand this code in depth. But do yourself a favor and have a look. The following code also plots all of the generated particle tracks on a single set of axes, each in a random color.
particleCount = 10;
N = 50;
tau = .1;
time = 0:tau:(N-1) * tau;
particle = { }; % create an empty cell array to hold the results
for i = 1:particleCount
particle{i} = struct();
particle{i}.dx = k * randn(1,N);
particle{i}.x = cumsum(particle{i}.dx);
particle{i}.dy = k * randn(1,N);
particle{i}.y = cumsum(particle{i}.dy);
particle{i}.drsquared = particle{i}.dx .^2 + particle{i}.dy .^ 2;
particle{i}.rsquared = particle{i}.x .^ 2 + particle{i}.y .^ 2;
particle{i}.D = mean( particle{i}.drsquared ) / ( 2 * dimensions * tau );
particle{i}.standardError = std( particle{i}.drsquared ) / ( 2 * dimensions * tau * sqrt(N) );
end
clf;
hold on;
for i = 1:particleCount
plot(particle{i}.x, particle{i}.y, 'color', rand(1,3));
end
xlabel('X position (m)');
ylabel('Y position (m)');
title('Combined Particle Tracks');
hold off;
Displacement Squared
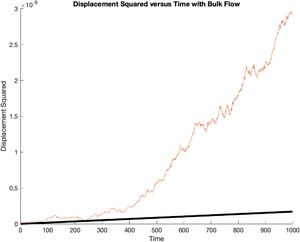
The following plot shows displacement squared versus time for all of the particles. The ensemble average of all the displacements is shown with a thick black line. The theoretical value of displacement squared is plotted with a thick blue line. Since displacement is expected to increase with the square root of time, displacement squared is a straight line in the plot.
% compute the ensemble average
rsquaredSum = zeros(1,N);
for i = 1:particleCount
rsquaredSum = rsquaredSum + particle{i}.rsquared;
end
ensembleAverage = rsquaredSum / particleCount;
% create the plot
clf;
hold on;
plot(time, (0:1:(N-1)) * 2*k^2 , 'b', 'LineWidth', 3); % plot theoretical line
plot(time, ensembleAverage , 'k', 'LineWidth', 3); % plot ensemble average
legend('Theoretical','Average','location','NorthWest');
for i = 1:particleCount
plot(time, particle{i}.rsquared, 'color', rand(1,3)); % plot each particle track
end
xlabel('Time (seconds)');
ylabel('Displacement Squared (m^2)');
title('Displacement Squared vs Time');
hold off;
Estimated Value of D
This plot shows the computed value of D for each simulation with error bars. A thick blue line indicates the best overall estimate of D (the average of the D value from each simulation) along with error bars in green * WHICH HAPPEN TO BE WRONG -- NEED TO FIX *.
clear D e dx;
% extract the D value from each simulation and place them all into a single
% matrix called 'D'
for i = 1:particleCount
D(i) = particle{i}.D;
dx(i,:) = particle{i}.dx;
e(i) = particle{i}.standardError;
end
% compute the estimate of D and the uncertainty
averageD = mean(D)
uncertainty = std(D)/sqrt(particleCount)
% plot everything
clf;
hold on;
plot(averageD * ones(1,particleCount), 'b', 'linewidth', 3); % plot estimated D
plot((averageD + uncertainty) * ones(1,particleCount), 'g-', 'linewidth', 1); % plot upper error bar
plot((averageD - uncertainty) * ones(1,particleCount), 'g-', 'linewidth', 1); % plot lower error bar
errorbar(D,e,'ro'); % plot D values with error bars
xlabel('Simulation Number');
ylabel('Estimated Diffusion Coefficient');
title('Estimated Diffusion Coefficient with Error Bars')
legend('Average Value of D', 'location', 'NorthWest');
hold off;
averageD =
4.2886e-013
uncertainty =
2.3294e-014
Motion Statistics and Plots
This section looks at the statistical properties of the simulated data in more detail. In particular, it discusses:
- Uncertainty in the estimate of the mean value of a random variable from a population of samples
- The effect of squaring a normally distributed random variable
- The assumption of statistical independence of samples
A More Perfect Distribution


Did you notice that the distribution of random displacement values in the second section looked a little lopsided? Even with 1000 samples, there can be some noticeable deviations from the ideal distribution. A million samples looks quite a bit closer to the ideal.
hist(randn(1,1e3),25)
xlabel('Value');
ylabel('Frequency');
title('Histogram of Values for 1000 Samples of randn');
hist(randn(1,1e6),100)
xlabel('Value');
ylabel('Frequency');
title('Histogram of Values for 1000000 Samples of randn');
Sampling Uncertainty

This lab requires you to make an estimate of the average value of a random variable (actually, the square of a random variable) from a population of samples of that variable. The uncertainty in your estimate decreases with the square root of the number of samples, N. (That is, the standard error = 1/sqrt(N).)
This concept is illustrated in the following plot. To create the plot, fifty populations of N random samples are created for each value of N from 1 to 100. The mean value of each sample population is plotted with an 'x' versus N. The uncertainty appears to decrease as 1/sqrt(N) as expected. About two thirds of the values fall between the error bars (plotted in dark black).
Matlab note: check out the nested for loops used to create the plot.
clf; hold on;
for i= 1:100
for j = 1:50
y = randn(1,i);
m = mean(y);
plot(i,m,'x');
end
end
plot(1:100, 1./sqrt(1:100), 'k', 'LineWidth', 2); % plot upper error bar in dark black
plot(1:100, -1./sqrt(1:100), 'k', 'LineWidth', 2); % plot lower error bar in dark black
hold off;
xlabel('Population Size (N)');
ylabel('Population Mean');
title('Population Mean of Normally Distributed Random Variable versus Population Size');
What Happens when you Square a Random Variable?

We did not estimate D in the simulations from the x and y displacements directly. Instead, we computed the mean squared value of dx and dy. What is the distribution of the resulting value? Adding the squares of two normally distributed random variables results in a chi-squared distribution (with two degrees of freedom) whose mean value equal to the sum of the variances of each variable. Here is what the chi-squared distribution looks like:
dx = randn(1,1e6);
dy = randn(1,1e6);
drSquared = dx .^ 2 + dy .^ 2;
mean(drSquared)
var(dx) + var(dy)
clf;
hist(drSquared,100);
title('Chi Squared Distribution (2 DOF), 1000000 Samples');
ans =
1.9982
ans =
1.9982
Auto Correlation - A Closer Look at the Data

The simulations so far have assumed that we are in the overdamped limit, or the inertia-less regime. This assumption makes generating simulated trajectories very easy - all you have to do is add up a bunch of properly distributed random numbers. Of course, just because something is convenient doesn't mean it's true.
There are many statistical tests for independence and normality. (My personal favorite is the Kolmogorov-Smirnov test – but never before 5:00 PM.) Auto and cross correlation are a good place to start testing for independence. Autocorrelation looks for a relationship between a variable and its past or future values. Cross correlation looks for a relationship between two variables. Matlab has a built in function to compute auto and cross correlations called xcorr.
By construction, the simulated displacements are independent. The change in position at one time should exhibit no relationship at all to the change at any other time. This can be verified with xcorr. If x is a vector, xcorr(x) returns the correlation of x with itself for all possible offsets. The length of the resulting autocorrelation sequence is 2N+1. The middle value always stands out because x correlates perfectly with itself when there is no offset. Specifying the option 'coeff' causes the xcorr function to normalize this value to exactly 1 --perfect correlation.
Also notice that the autocorrelation sequence is symmetric about the origin.
clf;
c = xcorr(particle{1}.dx, 'coeff');
xaxis = (1-length(c))/2:1:(length(c)-1)/2;
plot(xaxis, c);
xlabel('Lag');
ylabel('Correlation');
title('Particle 1 x-axis Displacement Autocorrelation');
Cross Correlation
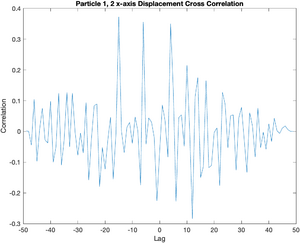
With two vector arguments, xcorr(x,y) returns a cross correlation matrix. The cross correlation can be used to test the relationship (or lack thereof) between one particle's trajectory and another's. If two particles move independently, the cross correlations should be very small. The code below computes the cross correlation between the x displacements of particle simulations number 1 and 2.
clf;
c = xcorr(particle{1}.dx, particle{2}.dx, 'coeff');
xaxis = (1-length(c))/2:1:(length(c)-1)/2;
plot(xaxis, c);
xlabel('Lag');
ylabel('Correlation');
Title('Particle 1, 2 x-axis Displacement Cross Correlation');
MATLAB Tricks

Matlab can generate (and plot) an amazing amount of data. For example, the xcorr function can compute the auto and cross correlations of a large set of data values. If A is an MxN matrix, xcorr(A) returns a size 2*M-1 x N^2 matrix whose columns contain the cross-correlation sequences for all combinations of the columns of A. The football shape of the data is a result of the way that the data is windowed when computing the correlation.
% create an array whose columns contain the dx values for each particle
for i = 1:particleCount
allDx(:,i) = particle{i}.dx';
end
% compute all possible auto and cross correlations
c = xcorr(allDx, 'coeff');
% plot the results
clf;
hold on;
for i=1:size(c,1)
plot(xaxis, c(:,i),'color',rand(1,3));
end
hold off;
xlabel('Lag');
ylabel('Correlation Coefficient');
title('All Possible Auto and Cross Correlations in the x Dimension');
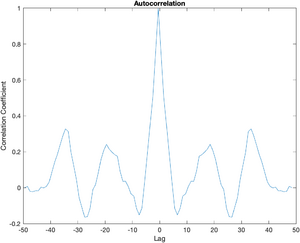
So what does the autocorrelation sequence look like for a trajectory that is not generated from independent samples? In the following example, the displacement at each time interval depends in part on the displacement in the last interval plus a random number. The autocorrelation is not nearly as sharp as the one generated by independent random samples.
x = zeros(1,N);
c = 0.80; % degree of correlation; 0 to 1
step = randn(1,N);
x(2) = randn();
for t=2:N
x(t) = (c * x(t-1)) + ((1-c)*step(t));
end;
clf;
plot(xaxis, xcorr(x, 'coeff'));
xlabel('Lag');
ylabel('Correlation Coefficient');
title('Autocorrelation');
Additional Resources
- Wolfram Alpha - Random Walk
- Democritus - MSD Theory
- MSD MATLAB Toolbox
- Mean Square Displacement Analysis of Single-Particle Trajectories with Localization Error: Brownian Motion in Isotropic Medium
- Active Diffusion Positions in the Nucleus
- Stochastic Diffusion


![{\displaystyle P[B(t+u)-B(t)\leq a]=\int _{x=-\infty }^{a}{\frac {1}{\sqrt {u2\pi }}}e^{-{\frac {1}{2}}({\frac {x}{\sqrt {u}}})^{2}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebbd74c792f8eaa66c2042fe6d7d2ce40e772fdb)





